import numpy as np  
import h5py  
import matplotlib.pyplot as plt  


plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots  
plt.rcParams['image.interpolation'] = 'nearest'  
plt.rcParams['image.cmap'] = 'gray'  



np.random.seed(1)
# GRADED FUNCTION: zero_pad  

def zero_pad(X, pad):  
    """
    Pad with zeros all images of the dataset X. The padding is applied to the height and width of an image,  
    as illustrated in Figure 1.

    Argument:
    X -- python numpy array of shape (m, n_H, n_W, n_C) representing a batch of m images
    pad -- integer, amount of padding around each image on vertical and horizontal dimensions

    Returns:
    X_pad -- padded image of shape (m, n_H + 2*pad, n_W + 2*pad, n_C)
    """  

    ### START CODE HERE ### (≈ 1 line)  
    X_pad = np.pad(X,((0,0),(pad,pad),(pad,pad),(0,0)),'constant',constant_values=(0,0))   
    ### END CODE HERE ###  

    return X_pad  
np.random.seed(1)  
x = np.random.randn(4, 3, 3, 2)  
x_pad = zero_pad(x, 2)  
print ("x.shape =", x.shape)  
print ("x_pad.shape =", x_pad.shape)  
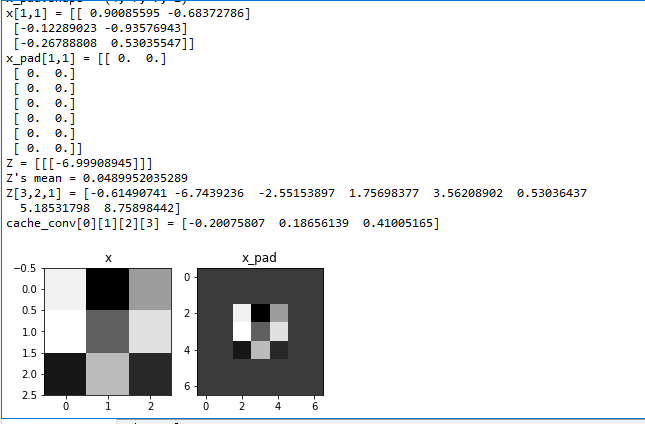
print ("x[1,1] =", x[1,1])  
print ("x_pad[1,1] =", x_pad[1,1])  

fig, axarr = plt.subplots(1, 2)  
axarr[0].set_title('x')  
axarr[0].imshow(x[0,:,:,0])  
axarr[1].set_title('x_pad')  
axarr[1].imshow(x_pad[0,:,:,0])
# GRADED FUNCTION: conv_single_step  

def conv_single_step(a_slice_prev, W, b):  
    """
    Apply one filter defined by parameters W on a single slice (a_slice_prev) of the output activation  
    of the previous layer.

    Arguments:
    a_slice_prev -- slice of input data of shape (f, f, n_C_prev)
    W -- Weight parameters contained in a window - matrix of shape (f, f, n_C_prev)
    b -- Bias parameters contained in a window - matrix of shape (1, 1, 1)

    Returns:
    Z -- a scalar value, result of convolving the sliding window (W, b) on a slice x of the input data
    """  

    ### START CODE HERE ### (≈ 2 lines of code)  
    # Element-wise product between a_slice and W. Do not add the bias yet.  
    s = a_slice_prev * W  
    # Sum over all entries of the volume s.  
    Z = np.sum(s)  
    # Add bias b to Z. Cast b to a float() so that Z results in a scalar value.  
    Z = Z+b  
    ### END CODE HERE ###  

    return Z  
np.random.seed(1)  
a_slice_prev = np.random.randn(4, 4, 3)  
W = np.random.randn(4, 4, 3)  
b = np.random.randn(1, 1, 1)  

Z = conv_single_step(a_slice_prev, W, b)  
print("Z =", Z)
# GRADED FUNCTION: conv_forward  

def conv_forward(A_prev, W, b, hparameters):  
    """
    Implements the forward propagation for a convolution function

    Arguments:
    A_prev -- output activations of the previous layer, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
    W -- Weights, numpy array of shape (f, f, n_C_prev, n_C)
    b -- Biases, numpy array of shape (1, 1, 1, n_C)
    hparameters -- python dictionary containing "stride" and "pad"

    Returns:
    Z -- conv output, numpy array of shape (m, n_H, n_W, n_C)
    cache -- cache of values needed for the conv_backward() function
    """  

    ### START CODE HERE ###  
    # Retrieve dimensions from A_prev's shape (≈1 line)    
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape  

    # Retrieve dimensions from W's shape  
    (f,f,n_C_prev,n_C) = W.shape  

    # Retrieve information from "hparameters" (≈2 lines)  
    stride = hparameters["stride"]  
    pad = hparameters["pad"]  

    # Compute the dimensions of the CONV output volume using the formula given above. Hint: use int() to floor. (≈2 lines)  
    n_H = int((n_H_prev+2*pad-f)/stride)+1  
    n_W = int((n_W_prev+2*pad-f)/stride)+1  

    # Initialize the output volume Z with zeros. (≈1 line)  
    Z = np.zeros((m,n_H,n_W,n_C))  

    # Create A_prev_pad by padding A_prev  
    A_prev_pad = zero_pad(A_prev,pad)  

    for i in range(m):                                 # loop over the batch of training examples  
        a_prev_pad = A_prev_pad[i,:,:,:]                     # Select ith training example's padded activation  
        for h in range(n_H):                           # loop over vertical axis of the output volume  
            for w in range(n_W):                       # loop over horizontal axis of the output volume  
                for c in range(n_C):                   # loop over channels (= #filters) of the output volume  

                    # Find the corners of the current "slice" (≈4 lines)  
                    vert_start = h*stride  
                    vert_end = h*stride+f  
                    horiz_start = w*stride  
                    horiz_end = w*stride+f  

                    # Use the corners to define the (3D) slice of a_prev_pad (See Hint above the cell). (≈1 line)  
                    a_slice_prev = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:]  
                    # Convolve the (3D) slice with the correct filter W and bias b, to get back one output neuron. (≈1 line)  
                    Z[i, h, w, c] = conv_single_step(a_slice_prev,W[:,:,:,c],b[:,:,:,c])  

    ### END CODE HERE ###  

    # Making sure your output shape is correct  
    assert(Z.shape == (m, n_H, n_W, n_C))  

    # Save information in "cache" for the backprop  
    cache = (A_prev, W, b, hparameters)  

    return Z, cache
np.random.seed(1)  
A_prev = np.random.randn(10,4,4,3)  
W = np.random.randn(2,2,3,8)  
b = np.random.randn(1,1,1,8)  
hparameters = {"pad" : 2,  
               "stride": 2}  

Z, cache_conv = conv_forward(A_prev, W, b, hparameters)  
print("Z's mean =", np.mean(Z))  
print("Z[3,2,1] =", Z[3,2,1])  
print("cache_conv[0][1][2][3] =", cache_conv[0][1][2][3])

运行结果：